Thoughtful research stays true to the data; assertions about differences in survey results need to be supported by tests of statistical significance. To advance that aim, we offer this margin-of-error calculator – our MoE Machine – as a convenient tool for data producers and consumers alike.
The tools below allow for calculation of the margin of sampling error in any result in a single sample; the difference needed for responses to a single question to be statistically significant (e.g., preference between two candidates, approve/disapprove or support/oppose); and the difference needed for statistical significance when comparing results from two separate samples.
We allow for the inclusion of design effects caused by weighting, which increase sampling error. Many publicly released polls understate their error margins by failing to include the design effect in their calculations. If you have the dataset, check the very bottom of this page for instructions on computing the design effect. If not, ask the researcher who produced the data you’re evaluating.
Calculations of a survey’s margin of sampling error require a probability-based sample, and do not address other potential causes of differences in survey results, such as question wording and noncoverage of the target population. And since MoE chiefly is a function of sample size, it’s important not to confuse statistical significance (easily obtained with big samples) with practical significance. Still, statistical significance comes first – if you don’t have it, you’re out of luck analytically.
These tools calculate MoE to the decimal. However, for customary sample sizes we recommend reporting MoE rounded to the half or whole number, to avoid implying false precision.
This is a beta version. Please send comments or trouble reports to info@langerresearch.com.
Basic MoE
Use this calculator to determine the margin of sampling error for any individual percentage, known as “p” (To calculate the margin of error for the survey overall, set “p” to 50 percent; this produces the most conservative calculation of MoE.) The yellow-shaded Margin of Error box will tell you the MoE associated with this percentage at the customary 95 percent confidence level.
| Margin of Error |
Confidence Level |
|---|---|
| 99% | |
| 95% | |
| 90% |
Definitions:
- Sample size = Total number of interviews, unweighted.
- p = The percentage being tested.
- q = The remainder of responses (will autofill).
- Design effect = A measure of how much the sampling variability differs from what it would be in a simple random sample (e.g., because of weighting). See calculation instructions at the bottom of this page.
- Population size = The size of the population being sampled. Use only when the sample is approximately 5 percent or more of the population (i.e., when the population is particularly small, or the sample size particularly large). Otherwise leave blank.
- Note: In public opinion research, the 95 percent confidence level typically is used (highlighted in yellow above). This calculator uses a two-tailed test.
Single-Item Test
For horse-race results and more. Use this calculator to see if differences in results from a single question are statistically significant – e.g., do more people approve or disapprove, support vs. oppose, or prefer Candidate A or Candidate B. In this calculator, p is the first percentage being tested (“approve,” let’s say) and q is the second percentage being tested (“disapprove”). The yellow-shaded box will tell you how big a difference between the two you need for statistical significance at the customary 95 percent confidence level. If the difference between your p and q exceeds this number, you’re golden. If not, your result just doesn’t cut it, significance-wise.
| Difference needed for statistical significance | Confidence Level |
|---|---|
| 99% | |
| 95% | |
| 90% |
z-value
p-value
Definitions:
- Sample size = Total number of interviews, unweighted.
- p = First percentage being tested.
- q = Second percentage being tested.
- Design effect = A measure of how much the sampling variability differs from what it would be in a simple random sample (e.g., because of weighting). See calculation instructions at the bottom of this page.
- Population size = The size of the population being sampled. Use only when the sample is approximately 5 percent or more of the population (i.e., when the population is particularly small, or the sample size particularly large). Otherwise leave blank.
- z-value = The calculated value of the z-test for statistical significance comparing p and q, based on a formula from this paper.
- p-value = The probability that, in multiple tests, you’d see a difference between p and q as big as the one the survey found, if there were no difference between p and q in the full population (the null hypothesis).
- Note: P-values less than .05 typically are required in public opinion research, indicating at least a 95 percent confidence level that the null hypothesis is rejected. P-values between .05 and less than .10, indicating at least a 90 percent confidence level, often are referred to as indicating “slight” differences. This calculator uses a two-tailed test.
Comparing Groups
Use this calculator to test for statistical significance in results among two groups in the same survey, or in results from one group in separate surveys (for example, when measuring apparent change over time). In this calculation, “p” is the percentage being tested – that is, whether the p in sample one (let’s say, the percentage of women who approve of the president’s job performance) differs significantly from the p in sample two (e.g., the percentage of men who approve). The yellow-shaded box gives you the difference between the first p and the second p needed for statistical significance at the customary 95 percent confidence level. If the difference between your p1 and p2 exceeds this number, you’ve got a statistically significant result. If not – sorry.
| Difference needed for statistical significance | Confidence Level |
|---|---|
| 99% | |
| 95% | |
| 90% |
z-value
p-value
Definitions:
- Sample size = Total number of interviews, unweighted.
- p = The percentages being tested.
- q = The remainder of responses (will autofill)
- Design effect = A measure of how much the sampling variability differs from what it would be in a simple random sample (e.g., because of weighting). See calculation instructions at the bottom of this page.
- Population size = The size of the population being sampled. Use only when the sample is approximately 5 percent or more of the population (i.e., when the population is particularly small, or the sample size particularly large). Otherwise leave blank.
- z-value = The calculated value of the z-test for statistical significance comparing Sample 1 and Sample 2, based on a formula from this paper.
- p-value = The probability that, in multiple tests, you’d see a difference between p1 and p2 as big as the one the survey(s) found, if there were no difference between p1 and p2 in the full populations (the “null hypothesis“).
- Note: P-values less than .05 typically are required in public opinion research, indicating at least a 95 percent confidence level that the null hypothesis is rejected. P-values between .05 and less than .10, indicating at least a 90 percent confidence level, often are referred to as indicating “slight” differences. This calculator uses a two-tailedtest.
Estimating the Design Effect
To estimate the design effect due to weighting, when the sum of the weights for the population of interest is the same as the unweighted sample size, use the weighted mean of the weights.
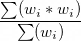
If the sum of the weights is not the same as the unweighted sample size, take the sum of the squared weights divided by the square of the summed weights and multiply the result by the sample size. (See Kalton et al. 2005.)
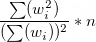
This is equivalent to the approach known as 1+L, expressed in the formula below, in which L is the squared “coefficient of variation” (cv) of the weights. The cv is the standard deviation of the weights divided by their mean. The standard deviation of the weights is best estimated using the population formula rather than the sample formula, though for large sample sizes the difference is negligible.
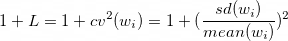
An estimated design effect enables you to calculate the effective sample size for the purpose of computing a margin of sampling error or power analysis. Simply divide the unweighted sample size by the estimated design effect. If you have a sample of 1,000 with an estimated design effect of 1.5, the effective sample size is 667 and the margin of sampling error for a proportion is 3.8 percentage points (assuming a 50/50 division), compared with 3.1 points for a sample size of 1,000 with a deff of 1.
Note that these estimates assume the worst-case scenario of no correlation between the weights and the outcome of interest, but also do not account for any additional variance potentially contributed by complex sampling features.
